The order of an internal node in a B+ tree index is the maximum number of children it can have. Suppose that a child pointer takes 6 bytes, the search field value takes 14 bytes, and the block size is 512 bytes. What is the order of the internal node?

What is the height of B+ tree with order-m & having N-keys?

Consider the given statements about B tree & B⁺ tree. When do you want to use B tree instead of B⁺ tree.

(i) When sequential access to key value is never required

(ii) When sequential access to key value is required

(iii) When Both sequential access & direct access is required

(iv) When direct access is required without sequential access

To construct a B⁺ tree, consider the following data

Data block size = 512 bytes, record Pointer as 7 bytes

Block Pointer = 6 bytes & search key value = 9 bytes

What’s the data of the B⁺ tree internal node

In section of data into B+ tree may cause

Constant a B⁺ tree for the following set of key values (2, 3, 5, 7, 11, 17, 19, 23, 29, 31)

Initially the tree is empty & values are added in the above given order. What will be the root of the connected B⁺ tree if the number of Points that will fit in one node is 6.

The worst case running time to search can element in a balanced Binary search tree with $n*2^n$element is

How many distinct BSTs can be created out of 4 distinct keys?

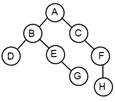
Consider the following Binary Tree given below. what is the successor of node G in in-order:

A function f defined on stacks of integers satisfies the following properties. f($\theta$) = 0 and f (push (S, i)) = max (f(S), 0) + i for all stacks S and integers i.

If a stack S contains the integers 2, -3, 2, -1, 2 in order from bottom to top, what is f(S)?

Convert the following infix expressions into its equivalent postfix expressions

(A + B ^ D) / (E – F) + G

What is a hash table?

To evaluate an expression without any embedded function calls:

The following postfix expression with single digit operands is evaluated using a stack:

              8 2 3 ^ / 2 3 * + 5 1 * -

Note that ^ is the exponentiation operator. The top two elements of the stack after the first * is evaluated are:

Suppose implementation supports an instruction REVERSE, which reverses the order of elements on the stack, in addition to the PUSH and POP instructions. Which one of the following statements is TRUE with respect to this modified stack?

Consider an implementation of unsorted single linked list. Suppose it has its representation with a head and a tail pointer (i.e. pointers to the first and last nodes of the linked list). Given the representation, which of the following operation can not be implemented in O(1) time?

Consider the function f defined below.

struct item

{

int data;

struct item * next;

};

int fun(struct item *p)

{

return (

(p == NULL) ||

(p->next == NULL) ||

(( P->data <= p->next->data) && fun(p->next))

);

}

For a given linked list p, the function f returns 1 if and only if

Given a hash table T with 25 slots that stores 2000 elements, the load factor α for T is __________

Let A be a square matrix of size n x n. Consider the following program. What is the expected output?

C = 100

for i = 1 to n do

for j = 1 to n do

{

Temp = A[i][j] + C

A[i][j] = A[j][i]

A[j][i] = Temp - C

}

for i = 1 to n do

for j = 1 to n do

Output(A[i][j]);

What is the correct syntax to declare a function foo() which receives an array of structure in function?