Q1:

In RLC circuits, the current at resonance is

Q2:

In a series R-L-C circuit, the maximum voltage across the capacitor occurs at frequency

Q3:

A resonance frequency of R-L-C series circuits draws maximum current due to the reason that,

Q4:

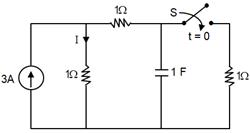
In the circuit given below, the steady state is attained with S open. S is closed at t = 0. What is the value of current I at t = 0⁺?

Q5:

In the circuit shown in the figure given below, the switch is opened at t = 0 after having been closed for a long time. What is the current through $50\Omega$resistor?

Q6:

Two resistance of $5\Omega$ and $10\Omega$and an inductor L are connected in series across a 50 cos $\omega$t voltage source. If the power consumed by the $5\Omega$resistor is $10\Omega$, the power factor of the circuit is

Q7:

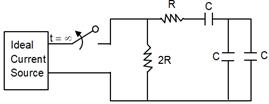
An ideal current source is connected to the disconnected circuit shown in the figure t = 0. The time constant of the circuit is

Q8:

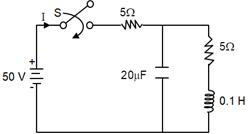
The network shown below is initially at rest. What is the initial current ${\rm I}$ when the switch S is closed at t = 0?

Q9:

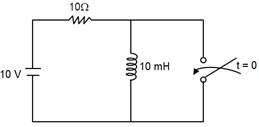
The circuit shown in the figure is in steady state, when the switch is closed at t = 0. Assuming that the inductance is ideal, the current through the inductor at t = 0⁺ equals

Q10:

A voltage waveform v(t) = 12 t²  is applied across a 1 H inductor for t$\ge$0, with initial current through it being zero. The current through the inductor for $t\ge 0$ is given by

Q11:

In any network the current will be seen to be consisting of a forced current and a natural current. A forced current is

Q12:

Transients are caused because

1. the load is suddenly connected to or disconnected from supply

2. of the sudden change in applied voltage from one finite value to the other

3. of the change in stored energy in inductors and capacitors

Q13:

There are no transients in pure resistance circuits because they

Q14:

What should be done to find the initial values of the circuit variables in a first-order R-C circuit excited by only initial conditions?

Q15:

An ideal voltage source will charge an ideal capacitor